Partie 1 : Recherche bibliographique

I. La théorie de l’information

1. Présentation générale

Les systèmes de traitement de l’information ont toujours utilisé des techniques de codage, bien avant l’informatique : les différents systèmes d’écriture, le Braille, le Morse, la sténo. Avec la généralisation de la numérisation de l’information sous toutes ses formes, il existe maintenant une grande variété de codes, adaptés à ses divers supports de transmission et de stockage (câbles coaxiaux, ondes hertziennes, disques magnétiques, CD-ROM, DCC, etc.).

Les codes sont conçus, en plus de la simple représentation de l’information, pour satisfaire à certaines exigences sur l’information codée : réduire sa taille (c’est la compression de données ), la rendre incompréhensible par des tiers (c’est la cryptographie ), permettre de reconstituer l’information initiale, même si elle a été altérée par un bruit (c’est la correction d’erreurs ). Dans ce projet nous nous intéresseront au codage de Huffman qui est un code de compression non destructif c’est à dire que les données décodées sont identiques à celles codées.

2. Le Codage de Huffman

Le codage de Huffman est un algorithme de compression qui fut mis au point en 1952 par David Huffman. C’est une compression de type statistique qui grâce à une méthode d’arbre que nous allons détailler plus loin permet de coder les octets revenant le plus fréquemment avec un code de bit beaucoup plus court. Cet algorithme offre des taux de compression assez bons et est utilisé dans de nombreux formats de compression (zip, jpg).

La compression de Huffman est un codage qui est une fonction inverse de la fréquence d’apparition. Plus un symbole apparaît et plus la longueur du code lui correspondant sera petite. En pratique on fait un tableau donnant le nombre d’apparition de chaque signe. On construit un arbre binaire en partant du bas. Les deux caractères les moins fréquents de la liste sont reliés à leurs parents en faisant la somme des comptes des fréquences. Les symboles prennent alors les valeurs 0 ou 1 qui sont retirées de la liste. Le processus est répété sur l’ensemble des caractères jusqu’à qu’il ne reste plus qu’un seul élément parent formant la racine de l’arbre. Pour décoder il suffit de redescendre et de noter les chemins parcourus pour arriver jusqu’aux feuilles et ainsi on obtient le caractère correspondant au code de Huffman. Une caractéristique essentielle du codage de Huffman est qu’il n’utilise pas de séparateur entre deux symboles. Chaque symbole est décodable de manière unique grâce à une technique de préfixe, c’est-à-dire si aucun mot du code n’est le préfixe d’un autre mot du code (par exemple 01 étant préfixe de 0111, ces deux mots ne peuvent appartenir à un code préfixe).

Cette méthode donne de bons résultats, mais souffre de quelques limites qui ont amené à le faire évoluer. Les contraintes sont :

• lecture préalable de l’ensemble des données
• construction de l’arbre binaire
• impossibilité de comprimer des données non connues à l’avance (page à « faxer »)
• transmission des codes employés pour la compression (le décompresseur doit connaître l’arbre pour reconstituer les données initiales)

Ces problèmes entraînent une perte de vitesse dans la compression et/ou la transmission et une dégradation du ratio de compression global.

Des solutions ont été envisagées pour améliorer les performances :

• construction d’un arbre de Huffman définitif (par exemple, on connaît les fréquences d’apparition des lettres de l’alphabet dans les textes en français)
• codage de Huffman dynamique (on construit un arbre à partir de répartitions théoriques des fréquences et on effectue une mise à jour dynamique au fur et à mesure que les informations sont traitées)

Remarque  : le codage de Huffman est inutile lorsque tous les caractères sont équiprobables.

II. La théorie de la programmation

1. Principe de l’algorithme

L’algorithme de Huffman peut pour la compression peut être décomposé en cinq étapes distinctes :

1. Faire la liste des symboles et les trier par nombre d’occurrences croissantes ; ces symboles constituent les feuilles de l’arbre de Huffman.
2. Prendre les deux nœuds de plus faible occurrence, les combiner en faire un nœud dont l’occurrence est égale à la somme des deux occurrences et marquer les nœuds fusionnés par 0 pour le premier et 1 pour le second (par ordre de probabilités décroissantes). Le nouveau nœud crée comportera les adresses les adresses des nœuds fils.
3. Répéter l’étape (2) jusqu’à ce qu’il ne reste qu’un seul nœud qui devient la racine de l’arbre binaire ainsi constitué.
4. Parcourir l’arbre depuis la racine jusqu’aux feuilles afin de déterminer les code de Huffman pour chaque caractère.
5. Lire le fichier à compresser en remplaçant chaque caractère par son codage de Huffman.

2. La construction de l’arbre

Une fois que les occurrences de chaque caractère présent dans les fichiers ont été déterminées, il faut construire l’arbre de Huffman. Pour cela on trie les caractères par occurrences et on crée un nœud qui pointe vers les deux plus petites. On insère ce nouveau nœud dans la liste avec comme occurrence la somme des occurrences des feuilles qu’il remplace. On répète l’opération jusqu’en avoir plus qu’un seul.

3. La compression

L’archive compressée se compose de 2 parties distinctes :

1. L’en-tête : contient toutes les données nécessaires à la décompression du fichier ainsi que des informations sur le fichier.
2. Les données : correspond à la transcription en symboles du fichier à compresser.

Durant cette phase les octets du fichier initial seront remplacés par leur code de Huffman correspondant.

4. La décompression

La décompression de fait en 2 étapes :

1. Dans un premier temps on extrait les informations contenues dans ‘en-tête afin de pouvoir reconstituer l’arbre qui a servi à la compression. (En cas de différence entre les arbres la décompression est impossible).
2. Une fois l’arbre reconstitué on effectue un décodage bit à bit du fichier.

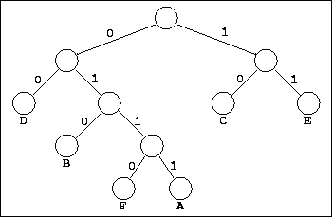
Le décodage d’un code préfixé se fait à l’aide d’un arbre. Il suffit de lire les symboles successifs du texte codé : si c’est un 0, on suit la branche de gauche, si c’est un 1, celle de droite ; quand on arrive à une feuille de l’arbre, on a décodé une lettre de la source ; on remonte alors à la racine et on continue avec le symbole binaire suivant. Il n’est pas nécessaire d’introduire un séparateur ou de décomposer en symboles.